TURUNAN ( I,II & III )

Nama   : Ahmad Rafiu Najwa Janahta

NPM    : 21312118

Kelas   : IF 21 C

TURUNAN  

Turunan adalah pengukuran terhadap bagaimana fungsi berubah seiring perubahan nilai yang dimasukan, atau secara umum turunan menunjukkan bagaimana suatu besaran berubah akibat perubahan besaran lainnya. Proses dalam menemukan turunan disebut diferensiasi.

Turunan atau Derivatif dalam ilmu kalkulus merupakan pengukuran terhadap bagaimana fungsi berubah seiring perubahan nilai masukan. Secara umum, turunan menyatakan bagaimana suatu fungsi berubah akibat perubahan variabel; contohnya, turunan dari posisi sebuah benda bergerak terhadap waktu adalah kecepatan sesaat objek tersebut.

Proses dalam menemukan turunan disebut diferensiasi. Kebalikan dari turunan disebut dengan antiturunan. Teorema fundamental kalkulus mengatakan bahwa antiturunan sama dengan integrasi. Turunan dan integral adalah operasi dasar dalam kalkulus.

Konsep turunan fungsi yang universal banyak sekali digunakan dalam bidang ekonomi untuk menghitung biaya marginal, total penerimaan dan biaya produksi, dalam bidang biologi untuk menghitung laju pertumbuhan mikroorganisme, dalam bidang fisika untuk menghitung kepadatan kawat, dalam bidang kimia untuk menghitung laju pemisahan, dalam bidang geografi untuk menghitung laju pertumbuhan penduduk dan masih banyak lagi.

Diferensiasi

Kemiringan fungsi linear ${\displaystyle m={\frac {\Delta y}{\Delta x}}}$

Dalam hal ini, y = f ( x ) = mx + b, untuk bilangan riil m dan b dan kemiringan m diberikan oleh

${\displaystyle m={\frac {{\text{mengalih pada }}y}{{\text{mengalih pada }}x}}={\frac {\Delta y}{\Delta x}},}$

Apa itu simbol ∆ adalah singkatan untuk perubahan. ${\displaystyle \Delta y=f(x+\Delta x)-f(x)}$

Rumus di atas berlaku karena

${\displaystyle {\begin{aligned}y+\Delta y&=f\left(x+\Delta x\right)\\&=m\left(x+\Delta x\right)+b=mx+m\Delta x+b\\&=y+m\Delta x.\end{aligned}}}$

Hasilnya adalah

${\displaystyle \Delta y=m\Delta x.}$

Nilai tersebut memberikan untuk kemiringan garis.

Nilai perubahan sebagai nilai limit

Gambar 1. Garis singgung pada (x, f(x))

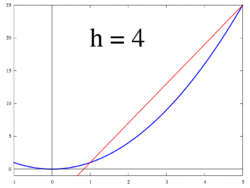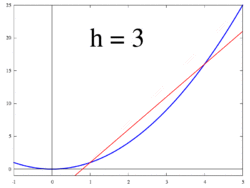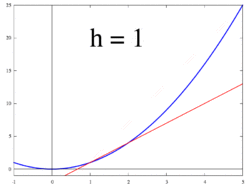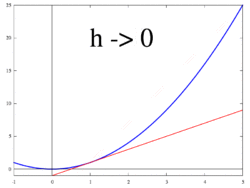
Gambar 2. The secant to curve y= f(x) determined by points (x, f(x)) and (x + h, f(x + h))

Gambar 3. Garis singgung sebagai batas garis potong

Gambar 4. Ilustrasi animasi: garis singgung (turunan) sebagai batas garis potong

Sifat - sifat turunan

Linearitas

• ${\displaystyle {\frac {d}{dx}}(u\pm v)=u'\pm v'\,}$
• ${\displaystyle {\frac {d}{dx}}(nu)=n{\frac {du}{dx}}\,}$

Aturan produk

• ${\displaystyle {\frac {d}{dx}}(uv)=u'v+uv'\,}$

Dalil rantai

• ${\displaystyle {\frac {dy}{dx}}={\frac {dy}{dv}}\cdot {\frac {dv}{du}}\cdot {\frac {du}{dx}}\,}$

Sifat umum lain

• ${\displaystyle {\frac {d}{dx}}({\frac {u}{v}})={\frac {u'v-uv'}{v^{2}}}\,}$
• ${\displaystyle {\frac {d}{dx}}(x^{n})=nx^{n-1}\,}$
• ${\displaystyle {\frac {d}{dx}}(u^{n})=nu^{n-1}\cdot {\frac {du}{dx}}}$

Dimana fungsi ${\displaystyle u}$ dan ${\displaystyle v}$ adalah fungsi satu variabel ${\displaystyle x}$.

Eksponen dan bilangan natural

• ${\displaystyle {\frac {d}{dx}}(e^{x})=e^{x}\,}$
• ${\displaystyle {\frac {d}{dx}}(a^{x})=a^{x}\ln {a}\,}$

Logaritma dan bilangan natural

• ${\displaystyle {\frac {d}{dx}}(\ln {x})={\frac {1}{x}}\,}$
• ${\displaystyle {\frac {d}{dx}}(\log _{a}{x})={\frac {1}{x\ln {a}}}\,}$

Trigonometri

• ${\displaystyle {\frac {d}{dx}}(\sin {x})=\cos {x}\,}$
• ${\displaystyle {\frac {d}{dx}}(\cos {x})=-\sin {x}\,}$
• ${\displaystyle {\frac {d}{dx}}(\tan {x})=\sec ^{2}{x}\,}$
• ${\displaystyle {\frac {d}{dx}}(\cot {x})=-\csc ^{2}{x}\,}$
• ${\displaystyle {\frac {d}{dx}}(\sec {x})=\sec {x}\tan {x}\,}$
• ${\displaystyle {\frac {d}{dx}}(\csc {x})=-\csc {x}\cot {x}\,}$

Invers

• ${\displaystyle {\frac {d}{dx}}(\arcsin x)={\frac {1}{\sqrt {1-x^{2}}}}}$
• ${\displaystyle {\frac {d}{dx}}(\arccos x)={\frac {-1}{\sqrt {1-x^{2}}}}}$
• ${\displaystyle {\frac {d}{dx}}(\arctan x)={\frac {1}{1+x^{2}}}}$
• ${\displaystyle {\frac {d}{dx}}(\operatorname {arccot} x)={\frac {-1}{1+x^{2}}}}$
• ${\displaystyle {\frac {d}{dx}}(\operatorname {arcsec} x)={\frac {1}{x{\sqrt {x^{2}-1}}}}}$
• ${\displaystyle {\frac {d}{dx}}(\operatorname {arccsc} x)={\frac {-1}{x{\sqrt {x^{2}-1}}}}}$

Hiperbolik

• ${\displaystyle {\frac {d}{dx}}(\sinh {x})=\cosh {x}\,}$
• ${\displaystyle {\frac {d}{dx}}(\cosh {x})=\sinh {x}\,}$
• ${\displaystyle {\frac {d}{dx}}(\tanh {x})={\text{sech}}^{2}\,{x}\,}$
• ${\displaystyle {\frac {d}{dx}}(\coth {x})=-{\text{csch}}^{2}{x}\,}$
• ${\displaystyle {\frac {d}{dx}}({\text{sech}}\,{x})=-{\text{sech}}\,{x}\tanh {x}}$
• ${\displaystyle {\frac {d}{dx}}({\text{csch}}\,{x})=-{\text{csch}}\,{x}\coth {x}}$

Sumber: https://id.wikipedia.org/wiki/Turunan

KALKULUS

A.Turunan

a)Aturan dasar turunan, sebagai berikut :1.Jika

f 

 (

 x

)

=

k 

, maka

f 

' 

(

 x

)

=

0

2.Jika

f 

 (

 x

)

=

 x

, maka

f 

' 

(

 x

)

=

1

3.Aturan Pangkat: Jika

f 

 (

 x

)

=

 X 

n

(

nε N 

)

, maka

f 

' 

(

 x

)

=

n. X 

n

−

1

4.Aturan Kelipatan Konstanta:

(

kf 

 )

' 

(

 x

)

=

k .f 

' 

(

 x

)

5.Aturan Jumla:

(

f 

 +

g

)

' 

(

 x

)

=

f 

 ' 

(

 x

)

+

g

' 

(

 x

)

!.Aturan "asil kali:

(

f . g

)

' 

(

 x

)

=

f 

' 

(

 x

)

.g

(

 x

)

+

f 

 (

 x

)

. g

' 

(

 x

)

#.

Aturan "asil bagi:

 

(

 f g

 )

' 

(

 x

)

=

f 

 ' 

(

 x

)

g

(

 x

)

−

f 

 (

 x

)

g

' 

(

 x

)

(

g

(

 x

)

 )

2

$.

Aturan %antai:

f 

 (

 x

)

=

u

n

→f 

' 

(

 x

)

=

n.u

n

−

1

.u' 

Contoh soal:

1)Tentukan

f ' 

 dari

2

 x

(¿¿

2

+

4

)

2

f 

 =¿

Ja&ab:

2

 x

(¿¿

2

+

4

)

2

f 

 =¿

2

 x

(¿¿

2

)

2

+

2.2

 x

2

.4

+(

4

)

2

f 

 =¿

f 

 =

4

 x

4

+

16

 x

2

+

16

f ' 

=

4.4

 x

4

−

1

+

16.2

 x

2

−

1

+

0

f 

' 

=

16

 x

3

+

32

 x